Задача 882
Дано натуральное число N. Требуется представить его в виде суммы двух натуральных чисел A и B таких, что НОД чисел A и B — максимален.
Задача 881
Из шахматной доски по границам клеток выпилили связную (не распадающуюся на части) фигуру без дыр. Требуется определить ее периметр.
Задача 880

 Исследовательская лаборатория одной известной автомобильной компании разработала специальный механизм, позволяющий повысить эффективность тормозов путем равномерной нагрузки деталей, используемых в тормозах.
Исследовательская лаборатория одной известной автомобильной компании разработала специальный механизм, позволяющий повысить эффективность тормозов путем равномерной нагрузки деталей, используемых в тормозах.
Одним из основных компонентов механизма являются 2 прокладки, которые в процессе взаимодействия накладываются друг на друга. Каждая прокладка длины n разделена на n разделов, каждый из которых имеет высоту h или 2h. Таким образом, прокладки имеют зубчатую форму без закруглений.
Тормозной механизм
В процессе взаимодействия прокладок важно, чтобы они накладывались друг на друга и при этом общая длина получившегося соединения была наименьшей.
Тормозной механизм
По заданной конфигурации прокладок требуется определить наименьшую длину их возможного соединения, при котором общая высота конструкции не превышает значения 3h. При этом вращать прокладки и удалять зубцы запрещено.
Задача 879
Напишите программу, которая ищущая все целые X, удовлетворяющие уравнению A*X^3 + B*X^2 + C*X + D = 0, где A, B, C, D – заданные целые коэффициенты.
Задача 878
 Для игры в калах используют несколько коробочек, расставленных по кругу, в которых лежат шарики. Ход осуществляется следующим образом. Берутся все шарики из одной коробочки, и начинают раскладываться по одному в коробочки подряд начиная со следующей по часовой стрелке. Если шариков больше, чем коробочек, то процесс продолжается (шарики раскладываются по второму кругу, по третьему и т.д.), пока не будут разложены все шарики. В коробочку, из которой взяли шарики, их тоже кладут. Пример одного хода приведен на рисунке. Справа шарики пронумерованы в том порядке, в котором они раскладывались по коробочкам.
Для игры в калах используют несколько коробочек, расставленных по кругу, в которых лежат шарики. Ход осуществляется следующим образом. Берутся все шарики из одной коробочки, и начинают раскладываться по одному в коробочки подряд начиная со следующей по часовой стрелке. Если шариков больше, чем коробочек, то процесс продолжается (шарики раскладываются по второму кругу, по третьему и т.д.), пока не будут разложены все шарики. В коробочку, из которой взяли шарики, их тоже кладут. Пример одного хода приведен на рисунке. Справа шарики пронумерованы в том порядке, в котором они раскладывались по коробочкам.
Петя, тренируясь перед соревнованиями, разложил шарики по коробочкам произвольным образом, и стал делать произвольные ходы. После каждого хода он записывал номер коробочки, в которую попадал последний шарик. В некоторый момент он решил восстановить начальную конфигурацию по конечной и по тем записям, которые он делал. Напишите программу, которая поможет ему в этом.
Задача 877
Требуется определить делимость на 7 ряда целых чисел, записанных в двоичной системе счисления.
Задача 876
Создайте массив, в котором кол-во отрицательных чисел равно кол-ву положительных и положительные числа расположены на случайных местах в массиве.
Задача 875
Заданы первый и второй элементы арифметической прогрессии. Требуется написать программу, которая вычислит элемент прогрессии по ее номеру.
Задача 874
Требуется написать программу, определяющую, в каких системах счисления с основаниями от 2 до 36 это число не содержит одинаковых цифр.
Задача 873
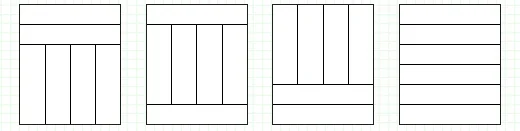 Прямоугольный коридор длиной N метров и шириной M метров решили застелить N прямоугольными плитками шириной 1 метр и длиной M метров, таким образом, чтобы не было не застеленной поверхности.
Прямоугольный коридор длиной N метров и шириной M метров решили застелить N прямоугольными плитками шириной 1 метр и длиной M метров, таким образом, чтобы не было не застеленной поверхности.
Требуется написать программу, которая найдет количество способов это сделать. Например, для коридора с размерами 6 на 4 существует четыре способа застелить плитками 1 на 4.
Задача 872
Требуется написать программу, определяющую, является ли натуральное число N палиндромом, т.е. одинаково читается слева направо и справа налево.
Задача 871
Необходимо вывести все простые числа от M до N включительно.
Задача 870
Заданы три числа: a, b, c. Необходимо выяснить, можно ли так переставить цифры в числах a и b, чтобы в сумме получилось c.
Задача 869
Дана строка, состоящая из N попарно различных символов. Требуется вывести все перестановки символов данной строки.
Задача 868
Два отрезка на плоскости заданы координатами своих концов в декартовой системе координат. Требуется определить, существует ли у них общая точка.
Задача 867
Дан набор из нескольких отрезков. Необходимо составить треугольник наибольшей площади, используя в качестве сторон три отрезка из заданных.
Задача 866
Требуется вывести представление целого числа N в виде произведения простых чисел.
Задача 865
Задан вес E пустой копилки и вес F копилки с монетами. В копилке могут находиться монеты N видов, для каждого вида известна ценность Pi и вес Wi одной монеты. Найти минимальную и максимальную суммы денег, которые могут находиться в копилке.
Задача 864
Даны размеры прямоугольных открытки и конверта. Требуется определить, поместится ли открытка в конверте.
Задача 863
Число называется совершенным, если оно равно сумме всех своих делителей, меньших его самого. Требуется найти все совершенные числа от M до N.