Задача 22
а квадратном торте размером N×N расставлено M свечей. Определить, можно ли одним прямолинейным разрезом разделить торт на две части, равные по площади, так, чтобы все свечи оказались на одной половине. Свечи считаем точками. Разрез не может проходить через свечу.
Задача 21
Реализовать функцию сортировки пузырьком через рекурсию.
Задача 20
Дано предложение. Заменить группы пробелов одним, крайние пробелы удалить. Все слова перевести в нижний регистр, первые буквы сделать заглавными.
Задача 19
Из текстового файла удалить все слова, содержащие 3-5 символов, но при этом из каждой строки должно быть удалено только четное количество таких слов.
Задача 18
Решить систему линейных алгебраических уравнений методом Холецкого.
Задача 17
Задано целое число. Выведите его значение в текстовом виде (например, одна тысяча двести тридцать четыре).
Задача 16
Дано натуральное число N. Найти все меньшие N числа Мерсена (Числа Мерсена определены формулой M = 2^p-1, где M и p - простые числа).
Задача 15
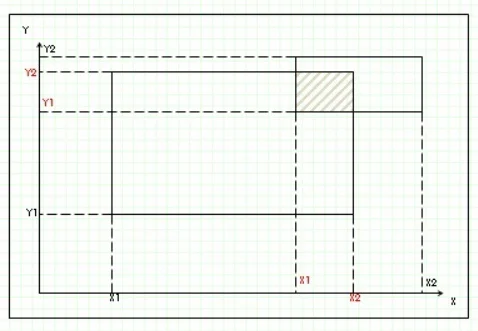Администрация города подбирает площадку для строительства новых спортивных сооружений. На рассмотрении несколько проектов, каждый проект требует выделения некоторого прямоугольного участка земли. Некоторые участки оказались частично или полностью в пользовании частными лицами, а в случае утверждения проекта администрация будет вынуждена выкупить этот участок, поэтому для определения стоимости очень важно знать площадь пересечения участков. Участки частников также прямоугольной формы (рис. 1) и стороны всех участков параллельны координатным осям. Для каждого проекта был построен план, включающий подобранный участок и его окружение. В приведенном примере показано пересечение участков частников (тонкая линия) с участком, подобранным для строительства (толстая линия). Помогите определить суммарную площадь пересечения участков частников с участком, выбранным для строительства. При этом следует учесть, что выкупаемая земля может принадлежать сразу нескольким участникам и в этом случае необходимо выкупать землю многократно (одна и та же площадь земли может быть посчитана несколько раз).
Задача 14
Сумма 1^1 + 2^2 + ... + 10^10 = 10405071317. Найдите последние десять цифр суммы 1^1 + 2^2 + 3^3 + ... + 1000^1000.
Задача 13
Известны результаты каждой из 4х четвертей баскетбольной встречи. Нужно определить победителя матча. Побеждает команда, набравшая больше очков в течение всего матч.
Задача 12
Определите сколько рулонов обоев нужно для комнаты с шириной A, длиной B и высотой C. Длина рулона - X, ширина Y.
Задача 11
Написать программу для кодирования данного текста с помощью азбуки Морзе.
Задача 10
Найдите наибольший общий делитель N натуральных чисел. Реализуйте два варианта: рекурсивный и без рекурсии.
Задача 9
Дана последовательность чисел 7, 11, 13, 14, 19, 21, 22, 25, …. Напишите программу, которая по заданному N находит N-ый член этой последовательности.
Задача 8
Дана дата в формате день:месяц:год. Определить дату через n дней.
Задача 7
Дан список. После каждого элемента добавьте предшествующую ему часть списка.
Задача 6
Напишите код для удаления дубликатов из несортированного связного списка.
Задача 5
Дано число М. Найти сумму и количество простых чисел, меньших М.
Задача 4
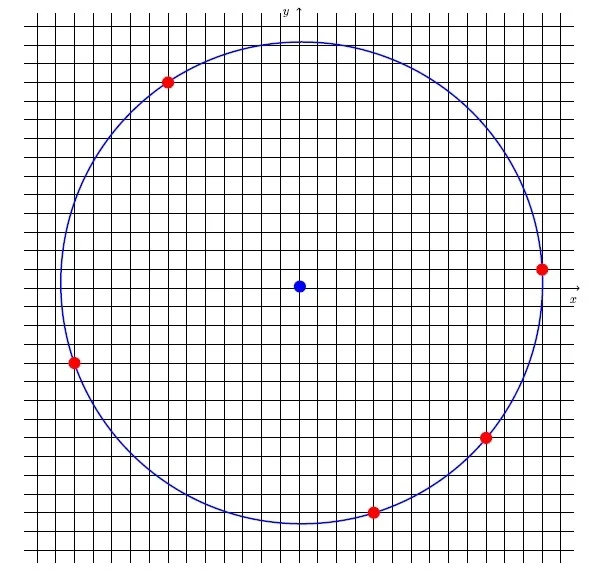Дан действительный радиус круга R и размер клетки L на клеточной бумаге. Известно, что центр круга находится на пересечении линий. Требуется найти число целых клеток, лежащих внутри круга. 0 ≤ R ≤ 25000, 1 < L < 100.
Задача 3
Дан текстовый файл. Создать новый файл, каждая строка - получается из соответствующей строки исходного файла перестановкой слов в обратном порядке.