Задача 1082
Астрономы часто изображают карту звездного неба на бумаге, где каждая звезда имеет декартовы координаты. Пусть уровнем звезды будет количество других звезд, которые расположены на карте не выше и не правее данной звезды. Астрономы решили узнать уровни всех звезд. Требуется определить, сколько звезд каждого уровня имеется на карте.
Задача 1081
Задачник содержит 300 задач, пронумерованных от 1 до 300. У учительницы есть магнитики с цифрами. В начале урока она прикрепляет их на доску так, чтобы образовались номера четырех задач, которые разбираются на уроке. Какое наименьшее число магнитиков должно быть у учительницы, чтобы она могла задать на уроке любые четыре задачи?
Задача 1080
Национальная сборная команда формируется из 20 игроков нескольких клубов. Известны номера игроков в своих клубах. Присвоить им номера в сборной так, чтобы максимальное количество игроков сохранило свои клубные номера. Все номера не превышают 20. Вводятся 20 номеров игроков в клубах. Напечатать в том же порядке 20 номеров игроков в сборной.
Задача 1079
Cоздать типизированный файл записей со сведениями о телефонах абонентов; каждая запись имеет поля: фамилия абонента, год установки телефона, номер телефона. По заданной фамилии абонента выдать номера его телефонов. Определить количество установленных телефонов с N-го года.
Задача 1078
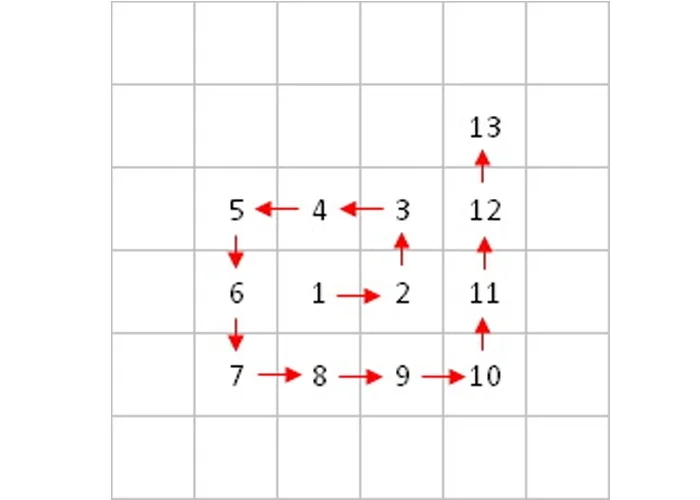Однажды математик С. Улам разделил лист бумаги на клетки и, написав в центре 1, начал писать по спирали против часовой стрелки все натуральные числа подряд, выделяя простые числа. Скоро простые числа выстроились в довольно-таки закономерном порядке, образуя интересный узор. Этот узор позже стал объектом исследования и получил название скатерть Улама.
Составьте программу, демонстрирующую скатерть Улама размером 100 х 100 клеток (вместо простых чисел выводите звездочку *).
Задача 1077
Номера троллейбусных билетов представляют собой шестизначные числа. Счастливым считается тот билет, у которого сумма первых цифр равна сумме трех последних цифр. Например, билет 627 294 считается счастливым, так как 6 + 2 + 7 = 2 + 9 + 4=15. Найдите все номера счастливых билетов, такие, что из них можно извлечь натуральный корень какой-либо (превышающей 1) степени. Например, √720801=849. Составьте программу для нахождения всех, номеров счастливых билетов, у которых сумма первых (последних) трех цифр, будучи возведенной в какую-либо степень, равна номеру счастливого билета.
Задача 1076
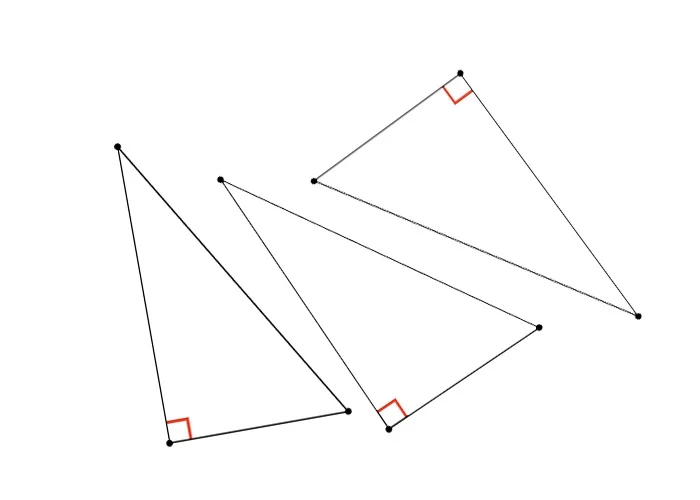Л. Кэрролл в своем дневнике писал, что он тщетно трудился, пытаясь найти хотя бы три прямоугольных треугольника равной площади, у которых длины сторон были бы выражены натуральными числами. Составьте программу для решения этой задачи, если известно, что такие треугольники существуют. Напишите программу, которая находит все прямоугольные треугольники (длины стороны выражаются натуральными числами), площадь которых не превышает данного числа S.
Задача 1075
Уроки по математике проводятся через день. Если урок попадает на воскресенье, то переносится на понедельник. Пользователь вводит дату первого урока. Сгенерируйте расписание из дат на текущий месяц.
Задача 1074
Создать два стека и поменять информацию местами.
Задача 1073
Создать массив, который одинаково читается как слева направо, так и справа налево.
Задача 1072
Создать список из заданного количества элементов. Выполнить циклический сдвиг этого списка на N элементов вправо или влево.
Задача 1071
Определить, пройдет ли прямоугольный параллелепипед с ребрами A, B, C через прямоугольное окно с заданными сторонами.
Задача 1070
Напишите код для удаления дубликатов из несортированного связного списка.
Задача 1069
Есть список слов c однокоренными словами. Нужно отделить основные и однокоренные слова. Пример: осн. сл. – interest, произ. – interesting...
Задача 1068
Найти все совершенные числа до 10000. Совершенное число - это такое число, которое равно сумме всех своих делителей, кроме себя самого.
Задача 1067
Написать программу для кодирования введенного текста с помощью азбуки Морзе.
Задача 1066
Аня нарвала яблок и поровну раздала своим сестрам Оле, Маше и Тане, а что осталось, съела. Оля свои яблоки поделила между тремя сестрами, а что осталось, съела. То же самое сделали Маша и Таня. Сколько яблок оказалось у каждой сестры?
Составьте программу для решения задачи о дележе в общем случае, то есть для дележа яблок между n лицами (n — входное данное). Дележ осуществляется в соответствии с теми же правилами, что и дележ между четырьмя лицами. Укажите число лиц (максимальное число лиц определите при помощи константы), а количество яблок у каждого из них сохраните в массиве.
Задача 1065
Даны две развертки кубов, на гранях которых записаны натуральные числа. Определить, относятся ли эти развертки к одному и тому же кубу.
Задача 1064
Написать программу обхода шахматной доски конем, начиная с данной клетки. На каждой клетке конь должен побывать ровно один раз.
Задача 1063
Вывести на экран числа от 1000 до 9999 такие, что все цифры различны.